La armonía del universo

Kepler perdió la vista, la orientación, la energía. Navega ciego, acompañando a la Tierra en su viaje anual alrededor del Sol. Era un telescopio espacial que hasta 2018 miró hacia las profundidades de la galaxia en la búsqueda de planetas lejanos, pero el año pasado se quedó sin combustible, y desde entonces sigue allí, sin instrumentos ni misión, a la deriva en la soledad interplanetaria. Cuatrocientos años antes, el hombre del que tomó el nombre, Johannes Kepler, terminaba su libro Harmonices mundi, la obra más mística, especulativa y personal que haya escrito. El libro, publicado en 1619, sea quizás uno de los trabajos más extraños de la revolución científica. Un cóctel inverosímil de ideas medievales y pensamiento científico moderno. Fue también el inicio de su propia deriva solitaria a través de una Europa que se desplomaba ante una de las guerras más sanguinarias de la historia humana.

Kepler fue el último pitagórico. La escuela pitagórica de la antigua Grecia fundaba su visión del mundo en los números enteros. Estos determinaban, entre otras cosas, la consonancia de los intervalos musicales y la geometría de los astros en el cielo. Johannes Kepler, veintiún siglos más tarde, llevaba aún estas banderas, a las que agregaba la astrología y una profunda fe luterana. A la luz del mundo de hoy todo esto parece un caldo de cultivo sólo apto para la reproducción de la pseudociencia. Pero en tiempos de Kepler las cosas se veían de otro modo. El marco estético y unificador que envolvía esta visión fue clave para que de su mente surgieran algunas de las ideas más reveladoras del siglo XVII.

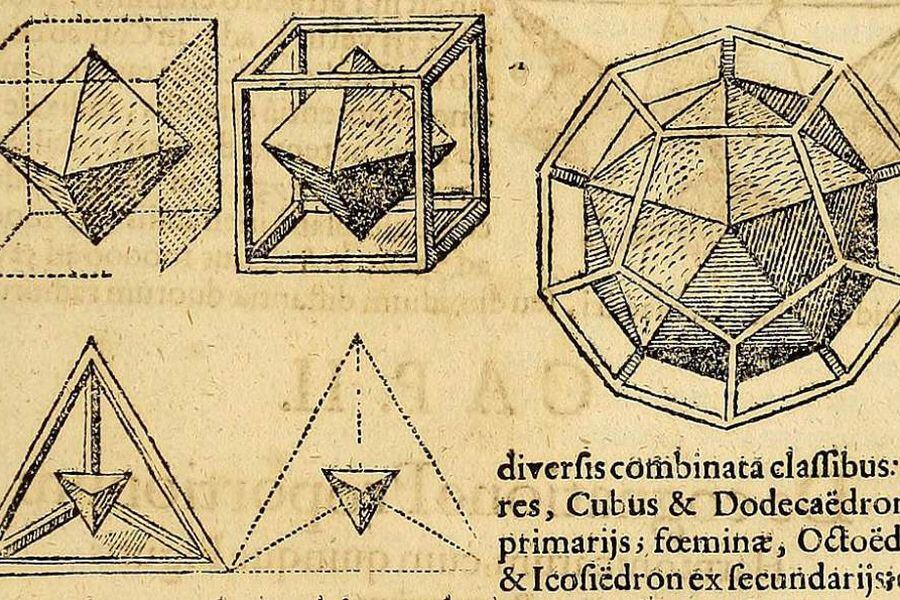
El 9 de julio de 1595, Kepler tuvo una epifanía. Enseñaba geometría ante una veintena de niños cuando los sólidos platónicos irrumpieron en su memoria. Estos son sólidos cuyas caras son idénticas. Por ejemplo, un cubo, que tiene seis caras iguales. El matemático griego Teeteto demostró en el siglo IV AC que sólo existían cinco sólidos platónicos; el tetraedro de 4 caras, el cubo de 6, el octaedro de 8, el dodecaedro de 12 y el icosaedro de 20. Si sólo hay cinco posibles sólidos platónicos, entonces al disponerlos uno dentro del otro, separarán el espacio en seis regiones. No podía ser coincidencia que sólo existieran seis planetas (entonces sólo se conocían Mercurio, Venus, la Tierra, Marte, Júpiter y Saturno). Era evidente que el Sol estaba rodeado por los cinco sólidos platónicos, y que los seis planetas tenían residencia en sus intersticios. Kepler no sólo podía predecir el número de planetas, sino que, inscribiendo un sólido sobre el otro en cierto orden determinado, podía predecir en forma aproximada la distancia al Sol de cada planeta. Esta teoría, demencial y bella, fue publicada en 1597 en su Mysterium Cosmographicum. Pero las discrepancias entre teoría y observación no podían ser subestimadas por uno de los padres de la ciencia. Sólo podría seguir avanzando en su gesta si conseguía más y mejores mediciones. Así fue como en 1600 comienza a trabajar para Tycho Brahe, el gran astrónomo danés.

Hasta hoy hay algo pitagórico en nuestra concepción del mundo. Ese uso de la matemática que hace que complejos fenómenos parezcan naturales inevitables. Desde el número seis de planetas de Kepler, hasta las nueve dimensiones espaciales de la teoría de supercuerdas. En este último caso hay muchos físicos que cifran esperanzas. La predicción de Kepler, sin embargo, fue derrumbada con el descubrimiento de Urano. Irónicamente, el telescopio espacial Kepler descubrió más de 2500 planetas fuera de nuestro sistema solar, más de la mitad de todos los que se han descubierto hasta el día de hoy.

Las discrepancias de la teoría de sólidos platónicos se agudizaron a la luz de los datos, mientras sus estudios sobre la órbita de Marte le permitieron publicar su segunda obra, Astronomia nova. Allí enuncia sus dos primeras leyes: las órbitas son elípticas y barren áreas iguales en tiempos iguales. Además sugiere que el Sol es el responsable, a través de una fuerza similar al magnetismo, de que los planetas se mantengan en órbitas, cuestión que Newton finalmente formularía con precisión.

Kepler demora en completar su Harmonices mundi. El mundo colapsaba a sus pies. Las protestas de los luteranos por la abolición de sus derechos terminaban en saqueos, incendios y defenestraciones. Lo que comenzó como una reivindicación de derechos religiosos terminó en la irracionalidad más brutal: la guerra de los 30 años, que acabó con la vida de 8 millones de personas. Kepler se aferró a sus poliedros, a sus melodías y a sus creencias para finalizar la obra. Allí, entre el canto de los planetas e intrincadas geometrías nace su tercera ley. Esa que nos permite relacionar el período de una órbita planetaria con la distancia a la estrella que la acoge. Con ella podemos calcular la longitud que separa a un planeta de su estrella. Entre otras cosas, esto nos ayuda a determinar cuántos de los miles de planetas lejanos que develó el telescopio Kepler podrían ser aptos para cobijar vida. Ahora podemos ser realistas al pensar en otros mundos más amables, mientras perdemos la esperanza en el nuestro. Kepler no podía concebir esos mundos, pero podía escaparse al suyo propio. Allí había siempre armonía, música y alegría. Por eso, cuando la irracionalidad lo invade todo, nada mejor que seguir sus consejos: "Cuando la tormenta se enfurece y el Estado es amenazado a naufragar, no podemos hacer nada más noble que echar el ancla de nuestros pacíficos estudios en el fondo de la eternidad".